GivenFunction \(\text{f(x)}=5\text{x}^\frac{3}{2}3\text{x}^\frac{5}{2}, x > 0\)TheoremLet f be a differentiable real function defined on an open interval (a, b)(i) If f'(x) > 0 for all x ∈ (a, b), then f(x) is increasing on (a, b) (ii) If f'(x) < 0 for all x ∈ (a, b), then f(x) is decreasing on (a, b) Algorithm(i) Obtain the function and put it equal to f(x)Problem 19 Easy Difficulty Find the intervals on which $f$ increases and the intervals on which $f$ decreases $$f(x)=x\cos x, \quad 0 \leq x \leq 2 \pi$$ Then y= f(x) >0 from ∞ to 4, which means that y= f(x) >0 over the interval (∞, 4) Remember that y is observed in the vertical axis, and a possitive value of y imply that is y is placed above the intersection with x axis (the intersection occurs in (x,y) = (0,0) On the other hand, when y is placed below the x axis, it takes negative

If F X 0 On An Interval Then F Is Concave Up On Chegg Com
F(x) 0 over the intervals (–∞ –3) and
F(x) 0 over the intervals (–∞ –3) and-B) on what intervals is f'(x) Example 12 Find intervals in which the function given by f (x) = sin 3x, x, ∈ 0, 𝜋/2 is (a) increasing (b) decreasing f(𝑥) = sin 3𝑥 where 𝑥 ∈ 0 ,𝜋/2 Finding f'(x) f'(𝑥) = 𝑑(sin3𝑥 )/𝑑𝑥 f'(𝑥) = cos 3𝑥 × 3 f'(𝒙) = 3 cos 3𝒙 Putting f'(𝒙) = 0 3 cos 3𝑥 = 0 cos 3𝑥 = 0 We know that cos θ = 0



Www Math Tamu Edu Mayaj Chapter5 Sec5p1completed Pdf
A helpful shorthand f ′ > 0 f ↑Let f (x) = x25(1−x)75,xϵ0,1 ⇒ f ′(x) =25x24(1−x)75 −75x25(1−x)74 = 25x24(1−x)74{(1−x)−3x} = 25x24(1−x)74(1−4x) We can see that f ′(x) is positive for x< 41 and f ′(x) is negative for x> 41This captures an intuitive property of continuous functions over the real numbers given f continuous on 1, 2 with the known values f(1) = 3 and f(2) = 5, then the graph of y = f(x) must pass through the horizontal line y = 4 while x moves from 1 to 2 It represents the idea that the graph of a continuous function on a closed interval can be drawn without lifting a pencil from the
Find The Intervals In Which The Function F Given By F X Sinx Cosx 0 X 2π Sarthaks Econnect The function f(x) = tan^ 1(sinx cosx), x > 0 is always an increasing function on the interval asked dec 22, 19 in limit, continuity and differentiability by rozy ( 418k points) applications of derivativesSolution for Find the intervals where f"(x) < 0 or f"(x) > 0 as indicated f"(x) < 0 (1, 0) O (1, 0) (00, 1) (1, 0), (1, o0) Answered Find the intervals where f"(x) < 0 or bartleby menu1 (this gets some marks) 8 < f(0) = 0 2e0 = 21 = 1
Solution for Given the graph 13 On what intervals of x is f(x) increasing?For x = 0 (1 6 k ) lo g (3 1 0 ) lo g 2;For x = 0 is continous at x = 0, then the value of k is




Oneclass 1 Point Letf X 2yx 6x For X Gt 0 Find The Open Intervals On Which Is Increasing
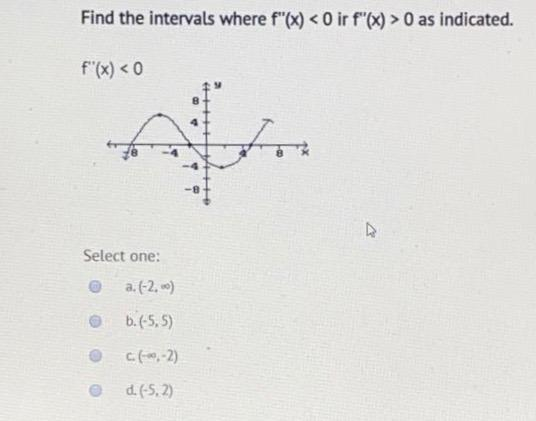



Find The Intervals Where F X 0 Ir F X 0 As Chegg Com
Using the Key Idea 3, we first find the critical values of f We have f ′ (x) = 3x2 2x − 1 = (3x − 1)(x 1), so f ′ (x) = 0 when x = − 1 and when x = 1 / 3 f ′ is never undefined Since an interval was not specified for us to consider, we consider the entire domain of f which is (− ∞, ∞)4x 2 ex = 0 Consider the function f(x) = 4x 2 ex Equivalently, we must show that f(x) = 0 for some x in the interval (0;More_vert Where on the interval 0, 4 does f ( x ) = 4 x – x 2 have a horizontal tangent line?
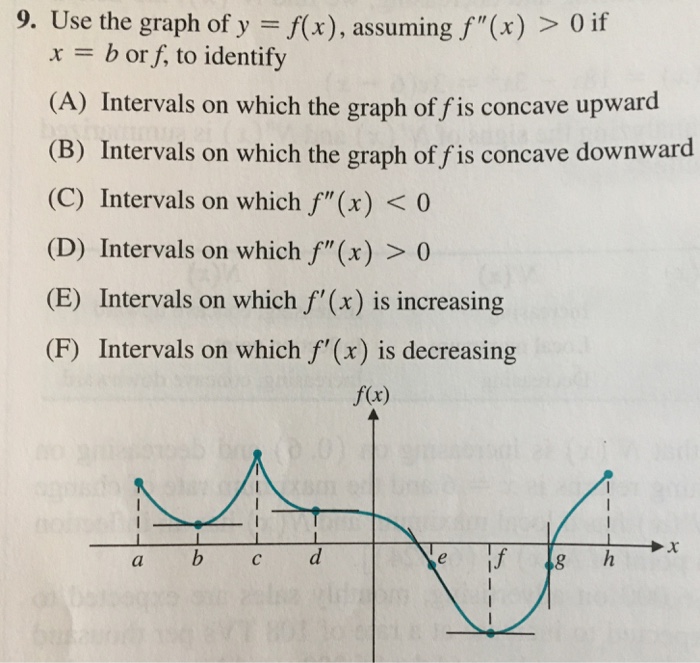



9 Use The Graph Of Y F X Assuming F X 0 If Chegg Com



F Vs F
Let $A(x)=\int_{0}^{x} f(t) d t$, with $f(x)$ as in Figure 12 Determine (a) The intervals on which $A(x)$ is increasing and decreasing (b) The values $x$ where $A(x)$ has a local min or max (c) The inflection points of $A(x)$ (d) The intervals where $A(x)$ is concave up or concave downIf f (x) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 1 − cos 8 x 2 0 x 3 x − 6 x − 1 0 x ;M−∞) such that f(x) ≤M(or f(x) ≥m, resp) for all x∈I So, fis bounded on Iif it is bounded both above and below on I We will be most interested in Ibeing an open or a closed interval Examples (1) Function f(x) = x2 is bounded on I= (−1,1) Indeed, we have 0 ≤f(x)



If F X X 4 8x 2 16 Then For Which Intervals Is F X Increasing Quora



Search Q F F F Graphs Tbm Isch
On the interval (1, 3), the function f(x) = 3x 2/x is (A) Strictly decreasing (B) Strictly increasing asked in Limit, continuity and differentiability by Rozy (Use n = 4 Solution First, divide the interval 0, 2 into n equal subintervals Using n = 4, Δx = (2 − 0) 4 = 05 This is the width of each rectangleDefinition of an increasing function A function f(x) is "increasing" at a point x 0 if and only if there exists some interval I containing x 0 such that f(x 0) > f(x) for all x in I to the left of x 0 and f(x 0) < f(x) for all x in I to the right of x 0




Interval Of F X Question Find The Intervals On Which F X 3x 4 4x 3 12x 2 2 Is My Working Out And Answer Correct Askmath
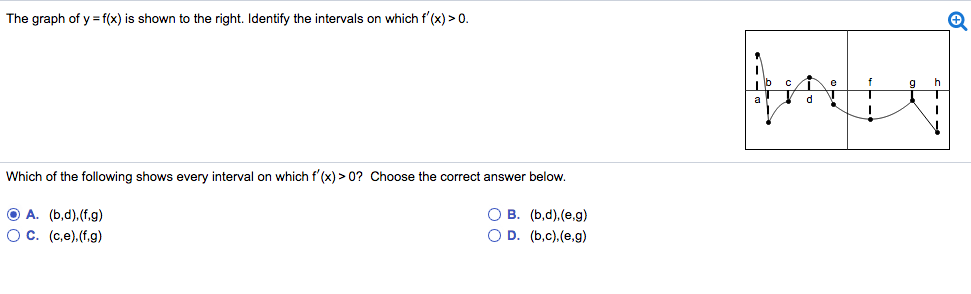



The Graph Of Y F X Is Shown To The Right Identify Chegg Com
Click here👆to get an answer to your question ️ The function f(x) = x^x decreases on the interval Join / Login Question The function f (x) = x x decreases on the interval A (0, e) B (0, 1) C 1 lo g x < 0 lo g x
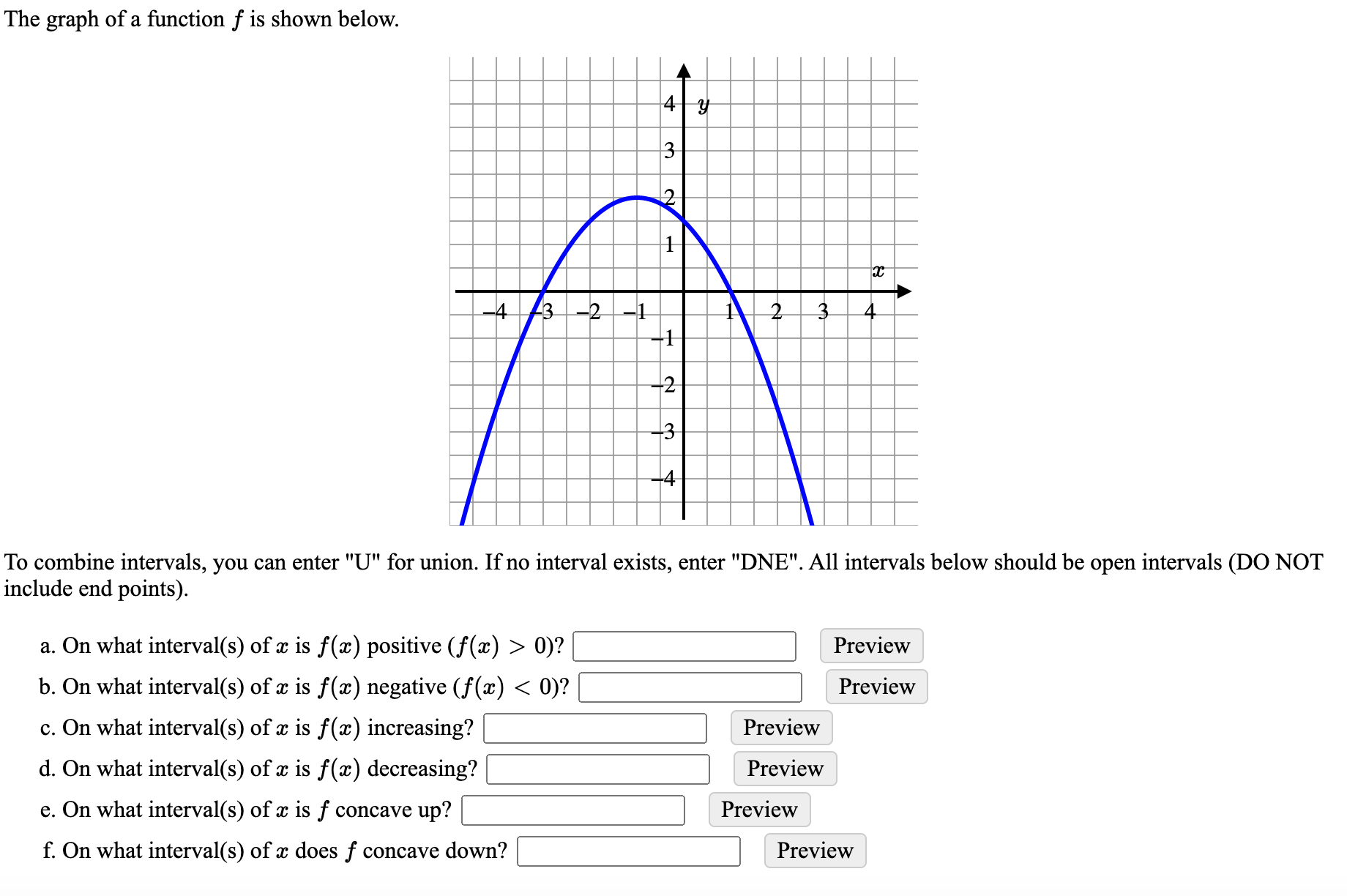



Answered The Graph Of A Function F Is Shown Bartleby




Use F X To Determine Intervals Where F X Is Increasing Or Decreasing Youtube
Answer to f'(3)= 0 and f'(0)=0 f'(x)>0 on the intervals (, f(0)=− f(x)0 only on the interval (−∞,−6) 9) Find an equation for a polynomial of degree 5 with the following properties zeros at x=4, and x=−6 f(0)=−13First we take the derivative f ′(x) = (x− 4 x2)′ = 1−4⋅(−2)⋅ x−3 = 1 8 x3 Note that f ′(x) = 0 at x = −2 The function and the derivative are undefined at x = 0, so there are two points that divide the real line (see figure above) Using the interval method, we determine the sign of the derivative



Http Www Mast Queensu Ca Math121 Assignments Unit06 Pdf



1
The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain If f′(x) > 0 at each point in an interval I, then the function is said to be increasing on I f′(x) < 0 at each point in an interval I, then the function is said to be decreasing on I Because the derivative is zero or does not exist only at critical points of theGet answer `f(x)=x(x4)^2,` interval `0, 4` Step by step solution by experts to help you in doubt clearance & scoring excellent marks in examsFor example, consider f(x) = x2 Notice that the graph of f goes downhill before x= 0 and it goes uphill after x= 0 So f(x) = x2 is decreasing on the interval (1 ;0) and increasing on the interval (0;1) Consider f(x) = sinx




Question Video Finding The Intervals Of Increasing And Decreasing Of A Function Involving Trigonometric Functions Nagwa



Solution Find Intervals On Which The Given Function Is Increasing And The Intervals On Which It Is Decreasing F X X 2 1 I 39 Ve Tried To Solve This And I 39 Ve Looked For Examples
Click here👆to get an answer to your question ️ Find the intervals in which f(x) = sin x cos x , where 0< x< 2pi is increasing or decreasing Use both leftendpoint and rightendpoint approximations to approximate the area under the curve of f(x) = x2 on the interval 0, 2;To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the intervals in which `f(x)=(x1)^3(x2)^2`is increasing or decreasing




A F X Lt 0 On The Interval X Lt 0 B F X Gt 0 On The Interval X Lt 0 C F X Lt 0 Brainly Com




Use The Graph Of F To Determine Where A F X 0 And Chegg Com
A) on what intervals is f'(x)>0? 0 $\begingroup$ Notice that the graph of $f$ crosses the $x$axis at $3,2,0,2$ and $3$ Using the fact $f(x)>0$ on the interval where the graph is above the $x$axis, and $f(x)0$ for $x\in (3,2)\cup(0,2)\cup(3,\infty)$If f′′(x) < 0 for all x ∈(a,b), then f is concave down on (a,b) Defn The point (x 0 ,y 0 ) is an inflection point if f is continuous at x 0 and if the concavity changes at x 0



Web Viu Ca Pughg Summer12 Math121m12n01 Secondderivativenotes Pdf



Function Intervals Of Increasing Or Decreasing Algebra House
F' (x) = 2x 3 = 0 2x = 3 x = 3/2 For x < 3/2, F' (x) < 0 and so F is decreasingExample 14 Define f 0,1 → Rby f(x) = (1/x if 0 < x ≤ 1, 0 if x = 0 Then Z 1 0 1 x dx isn't defined as a Riemann integral becuase f is unbounded In fact, if 0 < x1 < x2 < ··< xn−1 < 1 is a partition of 0,1, then sup 0,x1 f = ∞, so the upper Riemann sums of f are not welldefined An integral with an unbounded A F(x) < 0 on the interval x < 0 B F (x) > 0 on the interval x 0 on the interval 0 < x < 1
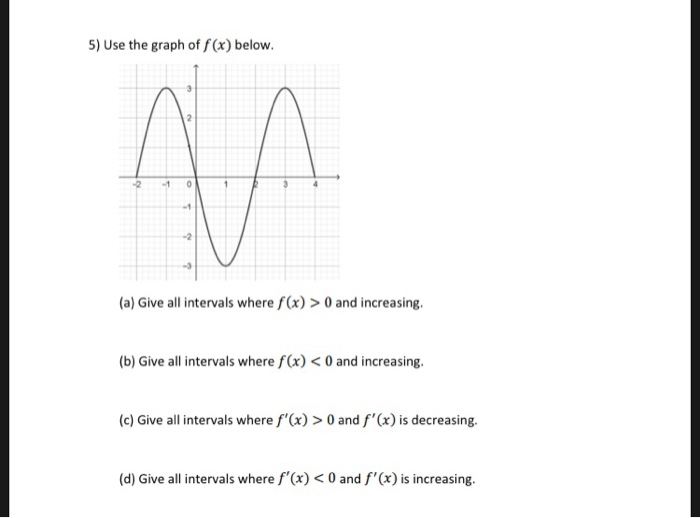



5 Use The Graph Of F X Below 1 0 2 A Give All Chegg Com
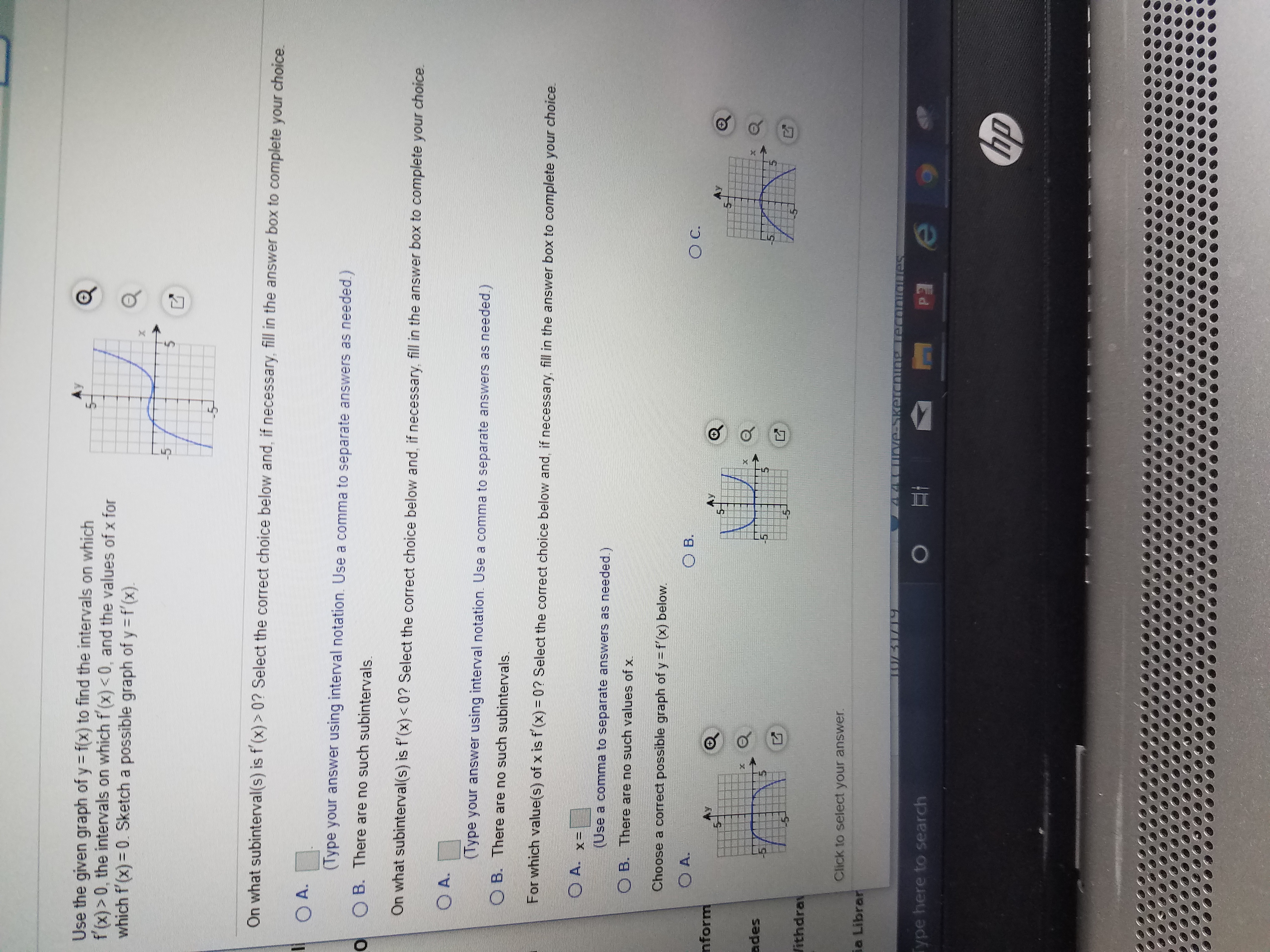



Answered Use The Given Graph Of Y F X To Find Bartleby
Let F (x) = x2 4x 1 Then F (3) = 2 < 0, and F (4) = 1 > 0Since F is continuous on 3,4, F (3) < 0, F (4) > 0, there is a point x in the interval 3,4 such that F (x) = 0, ie there is a root of F (x) = x2 4x 1 = 0 in the interval 3,4 Firstly, let me explain why this answer is correct f is a polynomial so f is continuous on the interval 0,3 f(0) = 2 and f(3) = 19 4 is between f(0) and f(3) so IVT tells us that there is a c in (0,3) with f(c) = 4 Finding the c requires solving x^3x^2x2 = 4 Which is equivalent to x^3x^2x6 = 0 Possible rational zeros are 1, 2, 3, and 6 Testing shows that 2 is a solution So c = 21) (this gets some marks) Because f is a ff of a polynomial and an exponential function, it is continuous everywhere, in particular, on the closed interval 0;



Increasing And Decreasing Functions
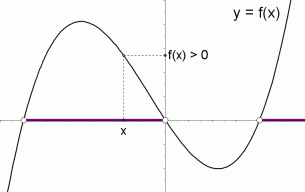



Graphical Interpretation Of Sentences Like F X 0 And F X 0
I would like to answer this more intuitively (less rigorously) The derivative of a function f(x) is basically the rate of change of f(x) with respect to x Thus if the derivative is negative, it implies that f(x) is not only changing with respectFirst week only $499!A f(x) < 0 on the interval x < 0 b f (x) > 0 on the interval x < 0 c f (x) < 0 on the interval 0 < x < 1 d f (x) > 0 on the interval 0 < x < 1
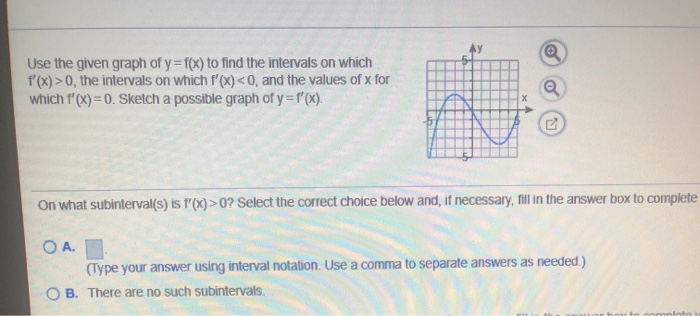



Use The Given Graph Of Y F X To Find The Intervals Chegg Com
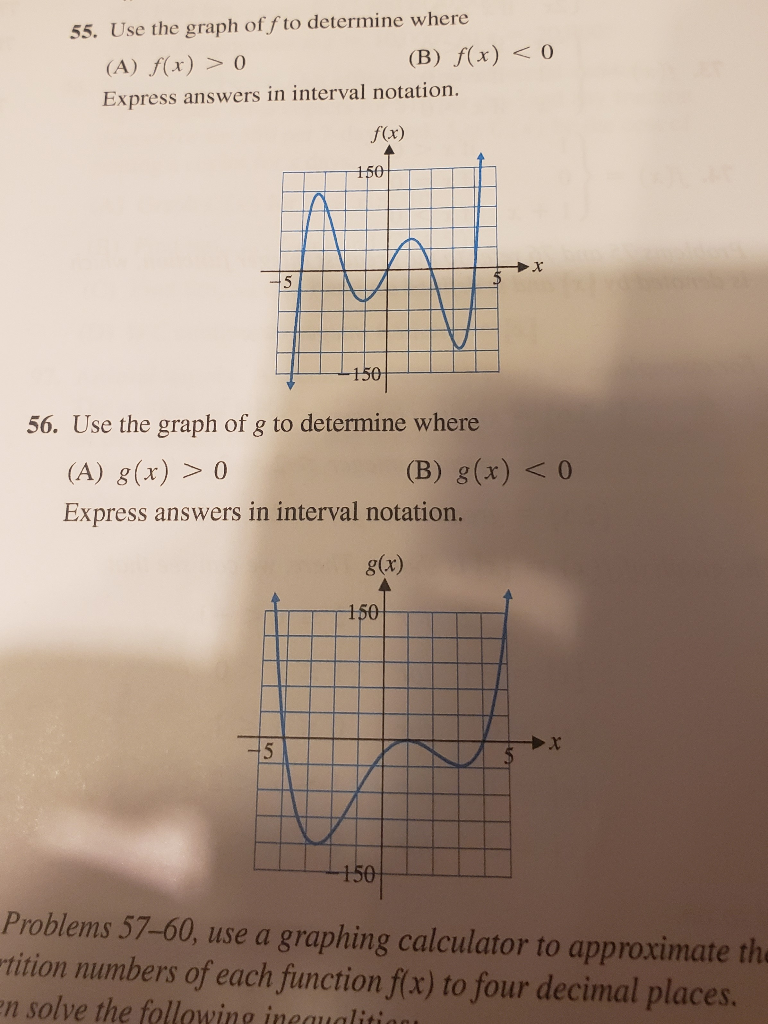



55 Use The Graph Of F To Determine Where A F X Chegg Com
If a function \(f\left( x \right)\) is differentiable on the interval \(\left( {a,b} \right)\) and belongs to one of the four considered types (ie it is increasing, strictly increasing, decreasing, or strictly decreasing), this function is called monotonic on this interval The concept of increasing and decreasing functions can also be defined for a single point \({x_0}\)Def bisection(f,a,b,N) '''Approximate solution of f(x)=0 on interval a,b by bisection method Parameters f function The function for which we are trying to approximate a solution f(x)=0 a,b numbers The interval in which to search for a solutionIf f ′ ( x) > 0 on an open interval, then f is increasing on the interval If f ′ ( x) < 0 on an open interval, then f is decreasing on the interval DO Ponder the graphs in the box above until you are confident of why the two conditions listed are true You should completely master this concept;
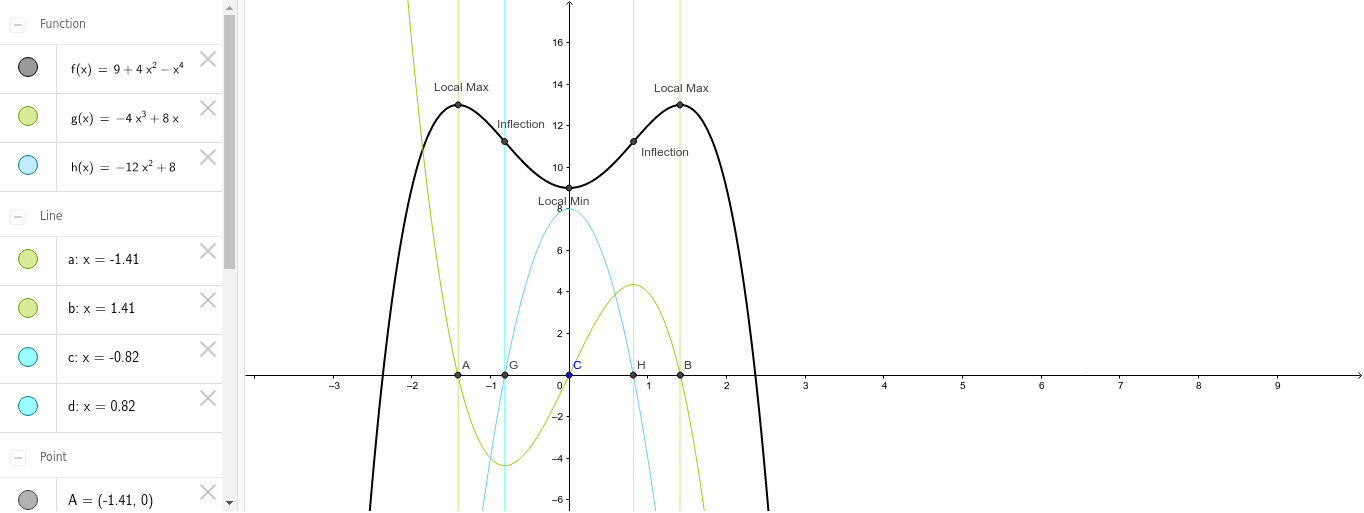



Yahoo Answers 04 09 Geogebra




Which Statement Is True About The Graphed Function F X Lt 0 Over The Intervals 0 7 And Brainly Com
Calculus Calculus Early Transcendentals (3rd Edition) Where on the interval 0, 4 does f ( x ) = 4 x – x 2 have a horizontal tangent line?On what intervals of x is f(x) positive?Close Start your trial now!




F X Lt 0 Over 3 And What Other Interval O 2 4 1 1 O 3 1 1 O 1 1 2 O 1 1 Brainly Com
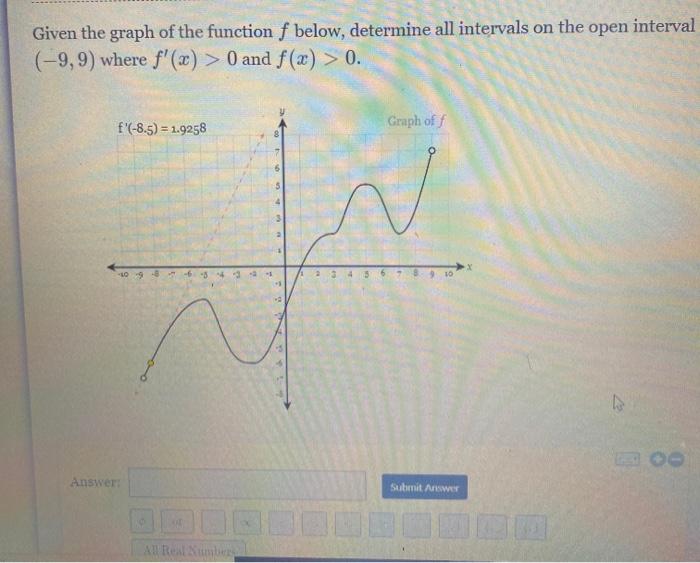



Given The Graph Of The Function F Below Determine Chegg Com
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Find the intervals in which the function `f` given by f(x) = sin x cos x, 0 `Solution f ′ ( x) = 3 x 2 − 6 x = 3 x ( x − 2) Since f ′ is always defined, the critical numbers occur only when f ′ = 0, ie, at c = 0 and c = 2 Our intervals are ( − ∞, 0), ( 0, 2), and ( 2, ∞) On the interval ( − ∞, 0), pick b = − 1A) If f'(x) >0 on an interval, then f is increasing on that interval b) If f'(x) 0 on an interval, then f is concave upward on that interval d) If f''(x)
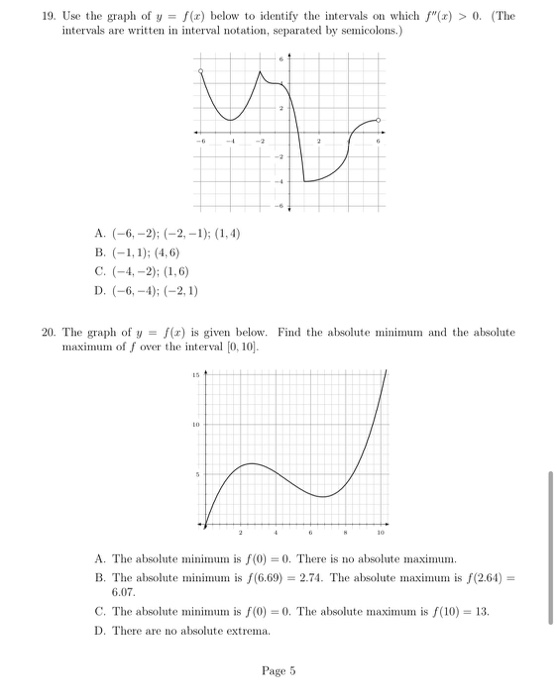



19 Use The Graph Of Y F X Below To Identify The Chegg Com



Www Math Tamu Edu Mayaj Chapter5 Sec5p1completed Pdf
Correct answer to the question A f(x) < 0 on the interval x < 0 b f (x) > 0 on the interval x < 0 c f (x) < 0 on the interval 0 < x < 1 d f (x) > 0 on the interval 0 < x < 1 e f (x) < 0 on the interv ∴ f'(x) > 0 f(x) is increasing on (0, 1) Since 0 < x < 157 099 < x99 < (157)99 0 × 100 < 100x99 < (157)99 × 100 0 < 100x99 < (157)99 × 100 Since 0 < x < 𝜋/2 So x is in 1st quadrant ∴ cos x is positive Thus, f(x) is strictly decreasing for none of the intervalsIf f′(x) > 0 on an interval, then f is INCREASING on that interval If f′(x) < 0 on an interval, then f is DECREASING on that interval A function has a LOCAL MAXIMUM at x = a if f(a) ≥ f(x) for all x "near" a
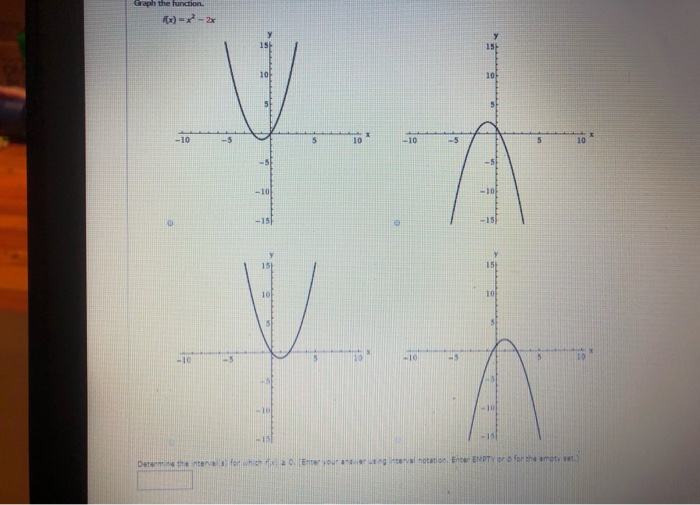



Determine The Interval S For Which F X 0 Enter Chegg Com



Search Q F X 3d 0 Tbm Isch
Answer to Find exact values for Riemann sums approximating the integral of the function f (x) = x^2 on the interval 0, 1 Split up the interval
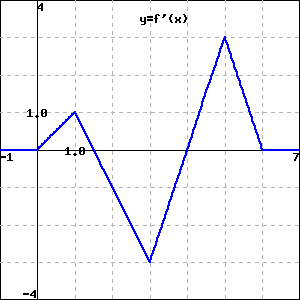



Preview 5 1 Abcdef Pg Query




Example 12 Find Intervals Where F X Sin 3x Is Decreasing




Use The Given Graph Of F X To Determine The Intervals Where F X Greater Than 0 F X Less Than 0 The X Values Where F X 0 And Where F X Is




The Graph Of Y F X Is Shown To The Right Identify Chegg Com



How Do You Determine Whether The Function F X Ln X 2 7 Is Concave Up Or Concave Down And Its Intervals Socratic




The Graph Of The Derivative F X Of A Function F Is Shown Below On What Intervals Is F Increasing Why On What Intervals Is F Decreasing Why If It Is Known That



Solving Polynomial Inequalities By Graphing




Answered Use The Graph Of F To Determine Each Of Bartleby
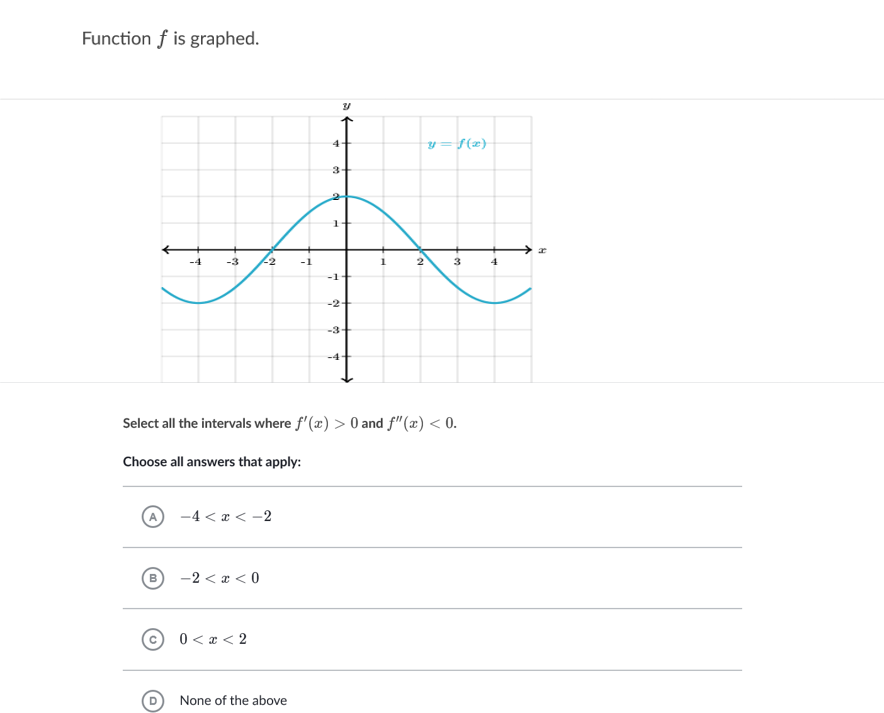



Function F Is Graphed Y F E 4 3 2 1 Select All Chegg Com




Use The Given Graph Of F X To Determine The Intervals Where F X 0 F X 0 And The X Values Where F X 0 And Where F X Is Undefined Then Sketch A Graph




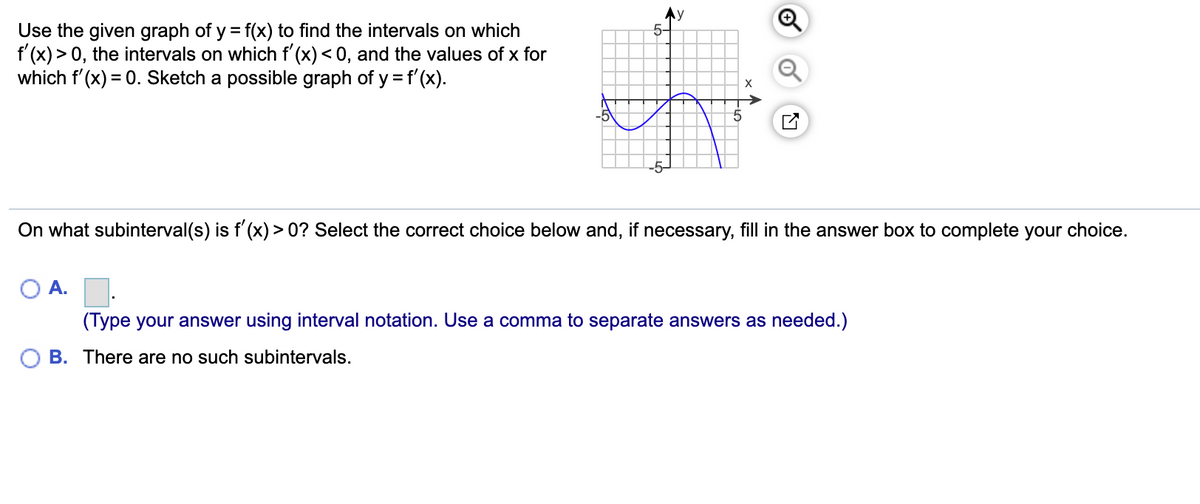
Use The Graph Of Y F X To Find The Intervals Of Which F X 0 The Intervals On Which F X 0 And The Values Of X For Which F X 0 Sketch A Possible Graph Of Y F X




Analyzing Graphs Flashcards Quizlet



Answered Ay 5 Use The Given Graph Of Y F X Bartleby



Features Of Function Graphs Mathbitsnotebook A1 Ccss Math



Use The Given Graph Of F X To Find The Intervals On Chegg Com




4 6 1 Polynomial And Rational Inequalities Part I




Select The Interval Where F X Gt 0 A 2 B 1 Lt X Lt 2 C 4 Help Brainly Com



Use The Given Graph Of F X To Find The Intervals On Chegg Com
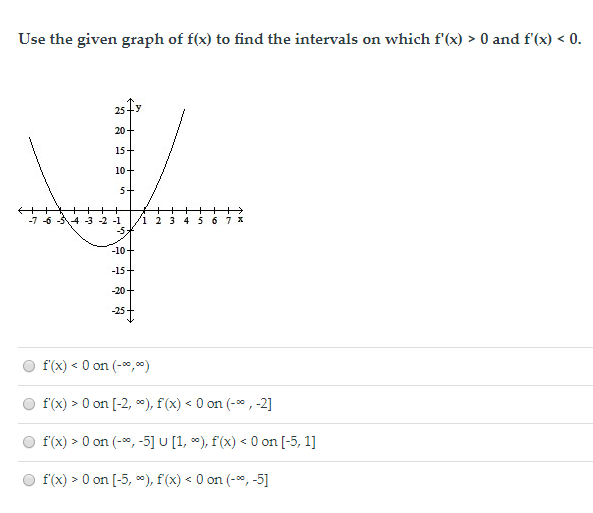



Use The Given Graph Of F X To Find The Intervals On Chegg Com
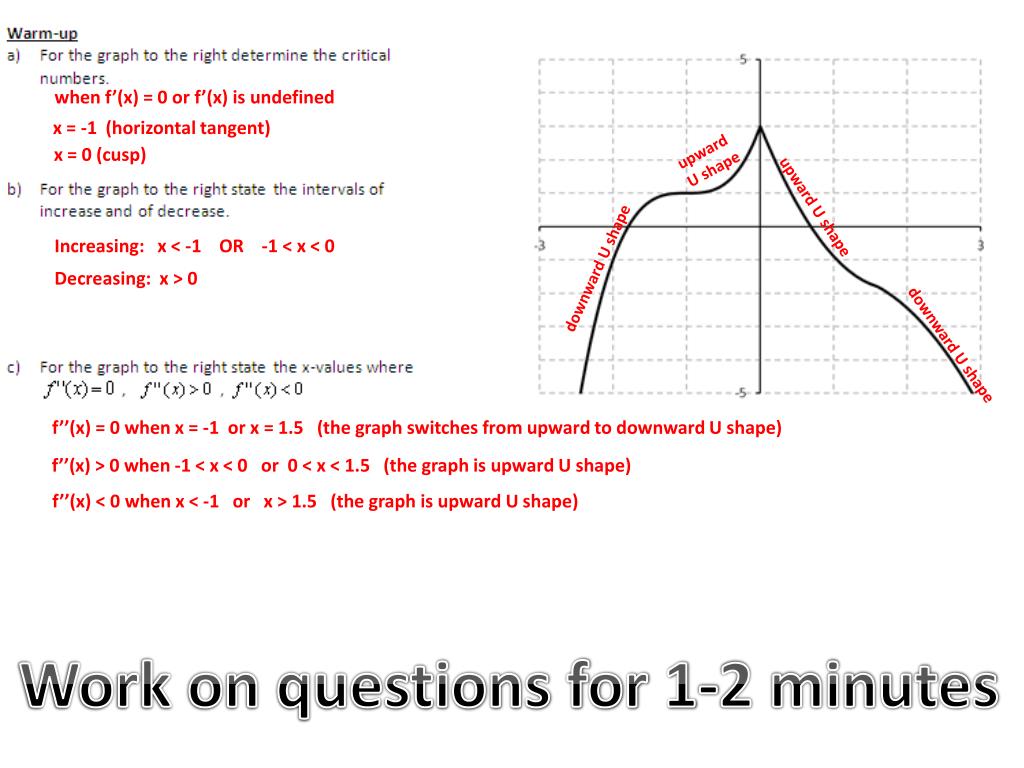



Ppt When F X 0 Or F X Is Undefined Powerpoint Presentation Id



Solution If F X X X 1 X 4 Use Interval Notation To Give All Values Of X Where F X Gt 0



Increasing And Decreasing Functions
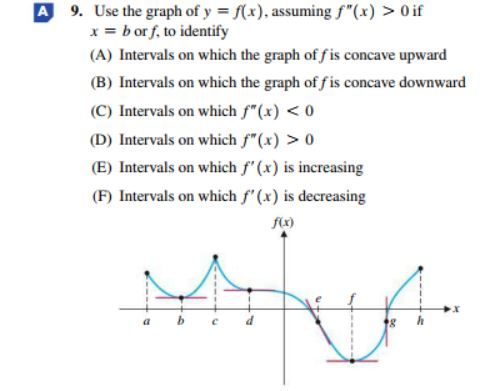



A 9 Use The Graph Of Y F X Assuming F X 0 If Chegg Com




Positive Negative Intervals Of Polynomials Article Khan Academy
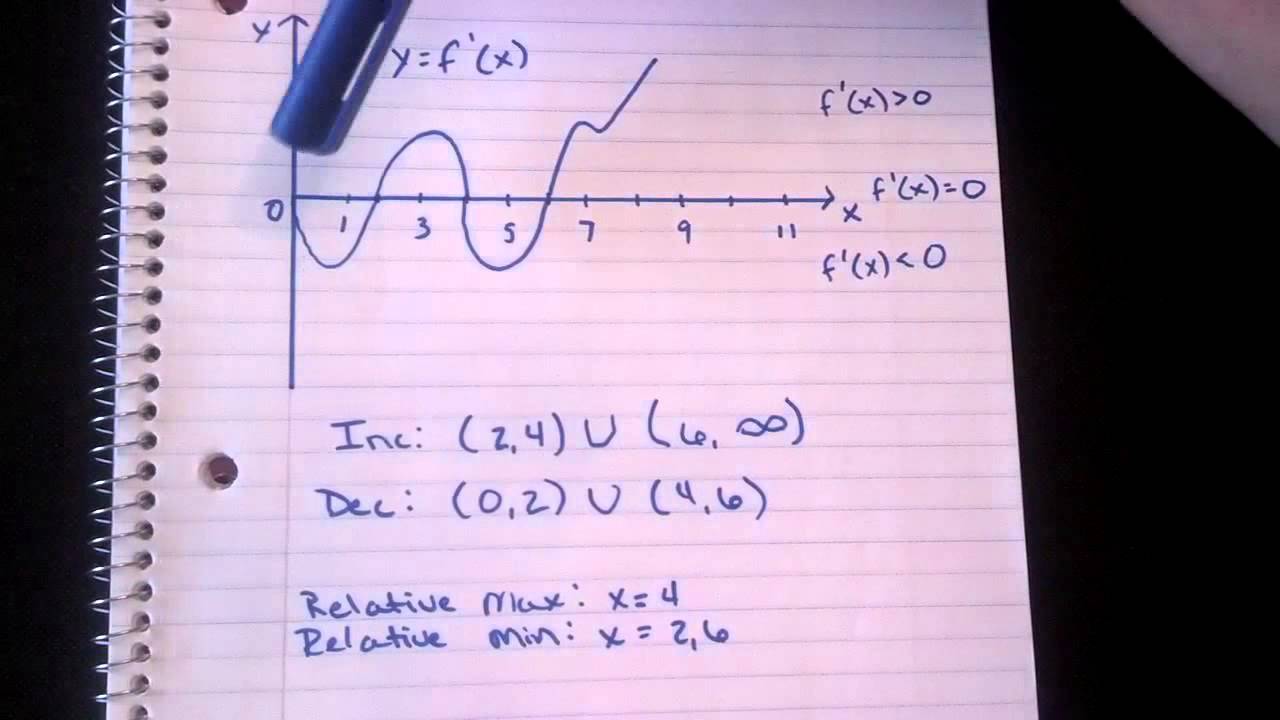



How To Use The Graph Of F To Identify The Intervals On Which F Is Increasing Or Decreasing Youtube



9 Infinite Intervals Infinite Function Values And Singularities Chebfun




Which Statement Is True About The Given Function A F X Lt 0 Over The Intervals Infinity 2 7 Brainly Com
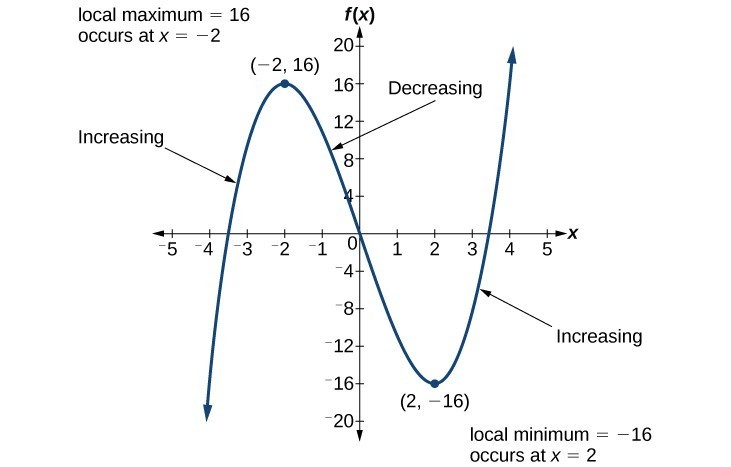



Use A Graph To Determine Where A Function Is Increasing Decreasing Or Constant College Algebra




A Determine The Intervals On Which X 0 And The Intervals On Which 34 X O Display Your Answer In The Form Of A Sign Chart For F 34 H Using Your Answer




Use The Given Graph Of F X To Find The Intervals On Chegg Com
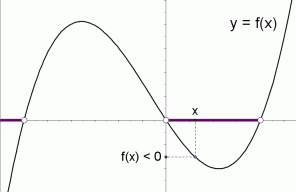



Graphical Interpretation Of Sentences Like F X 0 And F X 0
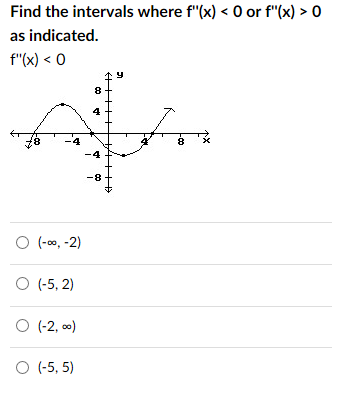



Find The Intervals Where F X 0 Or F X 0 As Chegg Com




How To Use Graph To Determine Where F X 0 And F X 0 Mathematics Stack Exchange
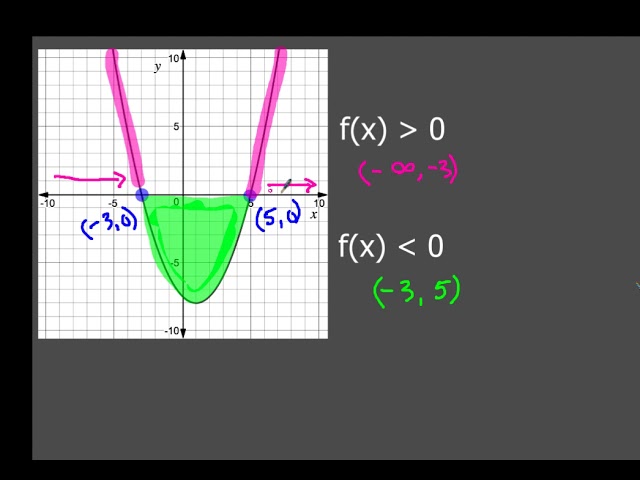



How To Tell Where F X Is Less Than 0 Or Greater Than 0 Youtube
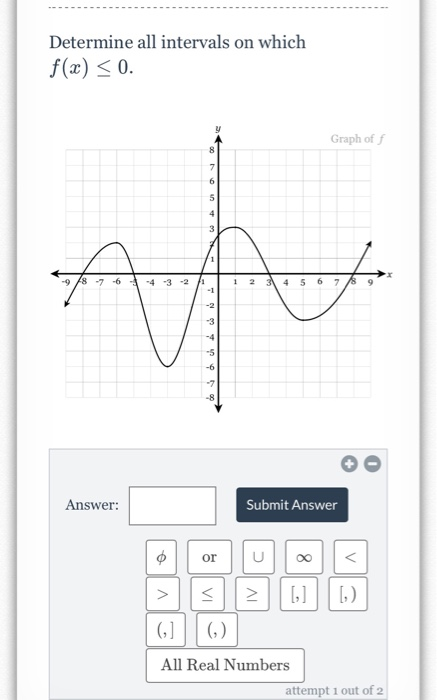



Determine All Intervals On Which F X 0 Graph Of 1 Chegg Com
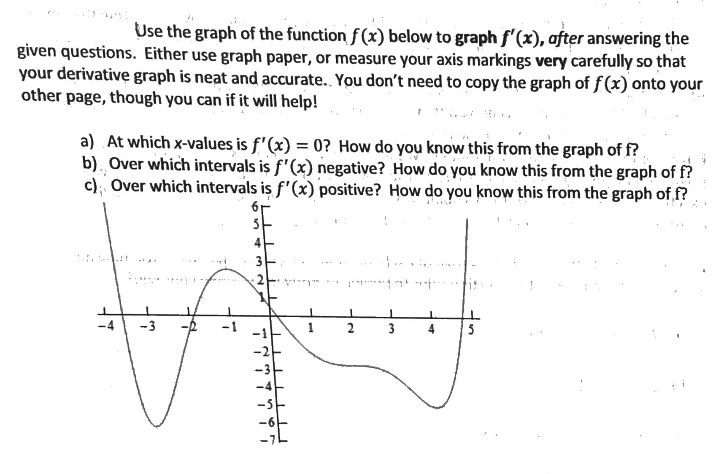



Answered A At Which X Values Is F X 0 How Bartleby
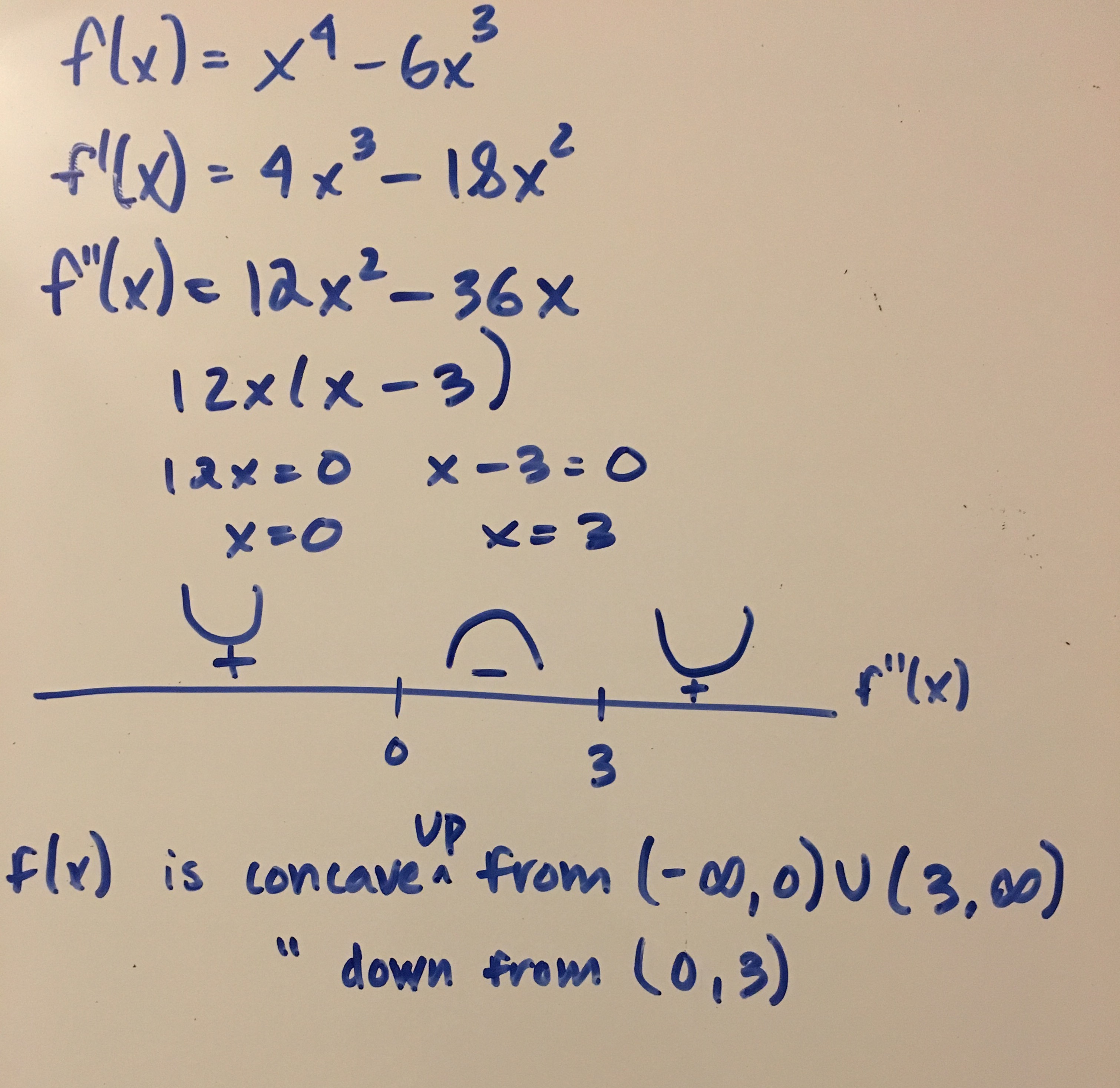



How Do You Ise Interval Notation Indicate Where F X Is Concave Up And Concave Down For F X X 4 6x 3 Socratic



Solved Use The Given Graph Of Y F X To Find The Intervals On Which 5 7 F X Gt 0 The Intervals On Which F X Lt 0 And The Values Of X Fo




Use The Given Graph Of F X To Determine The Intervals Where F X 0 F X 0 And The X Values Where F X 0 And Where F X Is Undefined Then Sketch A Graph




How Do I Write The Interval S For Which F X Is Greater Than Or Equal To 0 Interval Notation Brainly Com



Http Mysite Science Uottawa Ca Phofstra Mat1300 Lecture09 Pdf




Ex 6 2 3 Find The Intervals In Which F X Sin X Ex 6 2
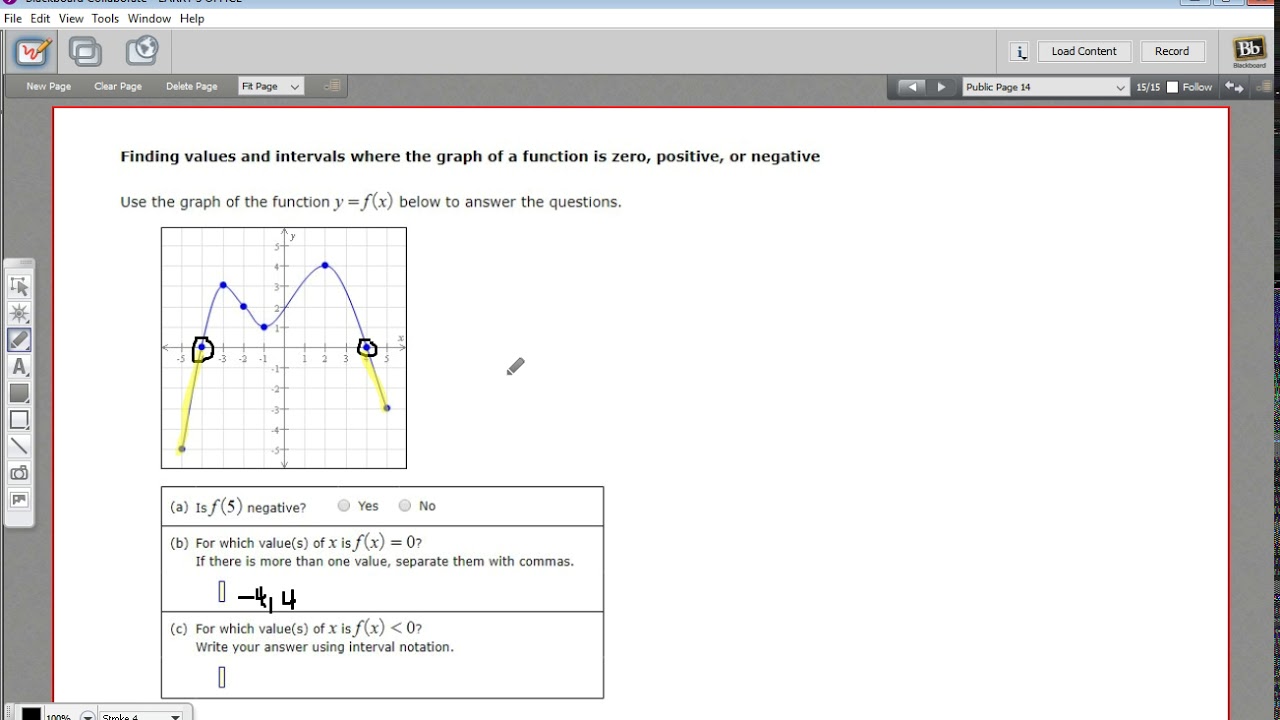



Finding Values And Intervals Where The Graph Of A Function Is Zero Negative Or Positive Youtube




Ex 2 Intervals For Which The First And Second Derivative Are Positive And Negative Given A Graph Youtube



Secure Media Collegeboard Org Digitalservices Pdf Ap Ap17 Calculus Q3 Pdf



Increasing And Decreasing Functions




Intervals For X 0 I By Cone N 2 000 A 05 Download Table




Piecewise Monotone Intervals Of F X X P Sin X 0 X 2p Download Scientific Diagram




Solved Which Statement Is True About The Graphed Function F X F X Lt 0 Over The Intervals Brainly Com




Predict Which Statements Are True About The Intervals Of The Continuous Function Check All That Brainly Com
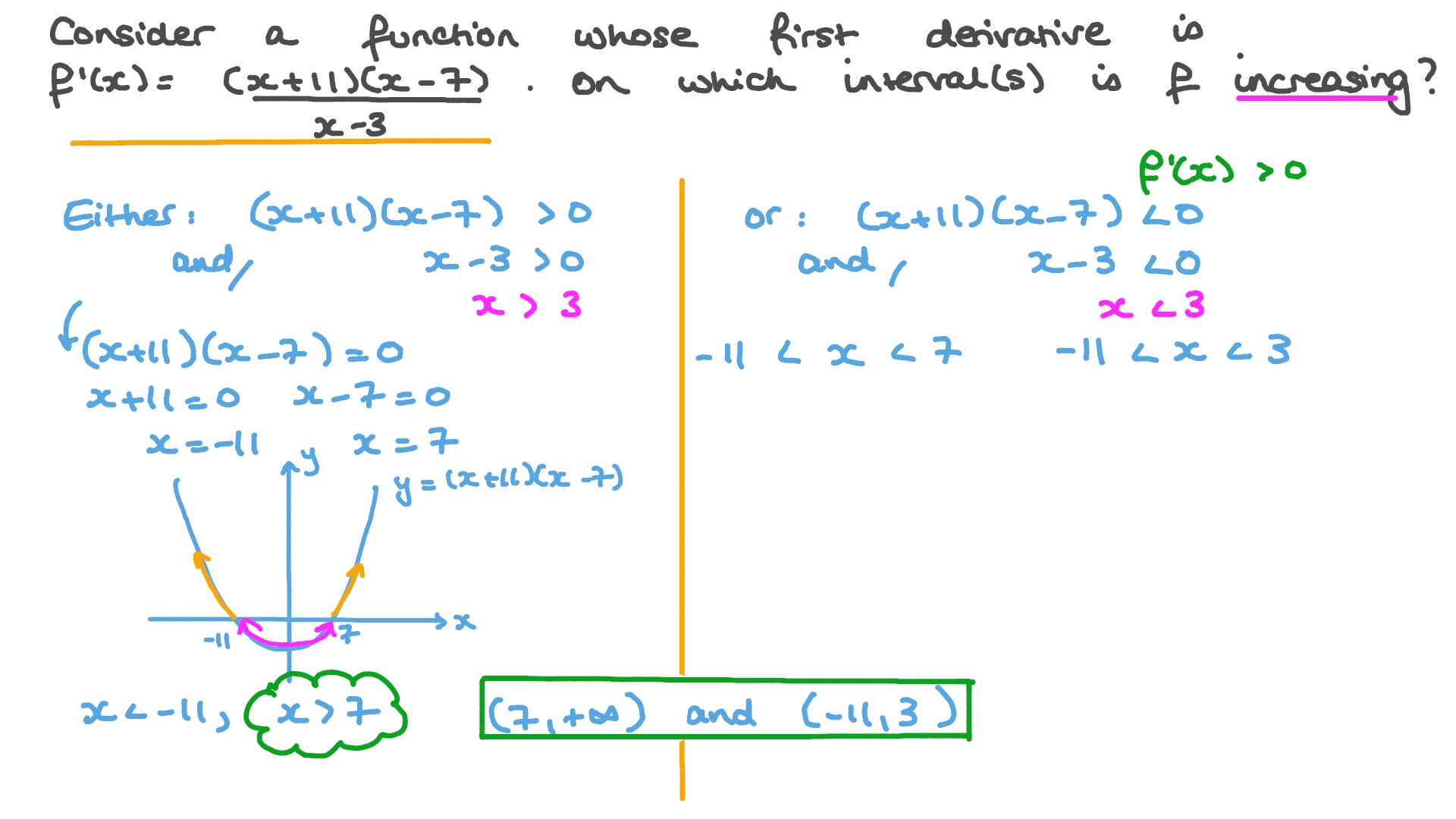



Question Video Finding Intervals Of Increase Of A Function Nagwa
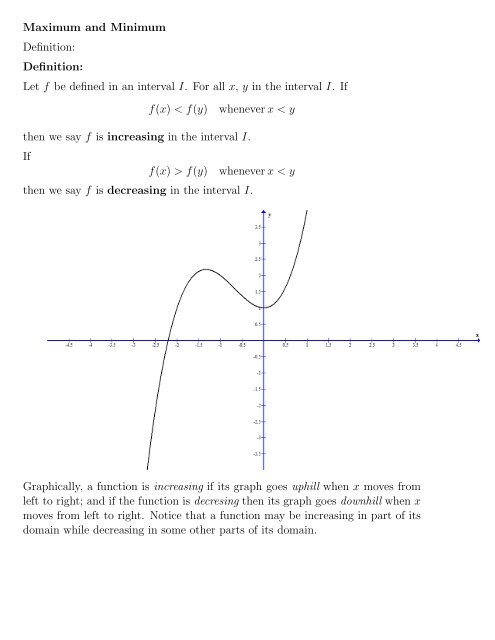



Let F Be Defined In An Interval I For All X Y In The Interval I




Find The Intervals In Which F X X 1 X 2 2 Is Increasing Or Decreasing Youtube
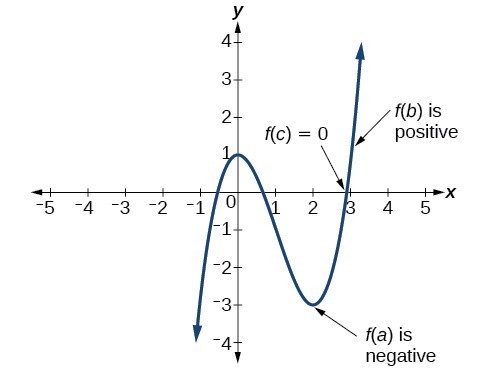



Use The Intermediate Value Theorem College Algebra



Interval Notation
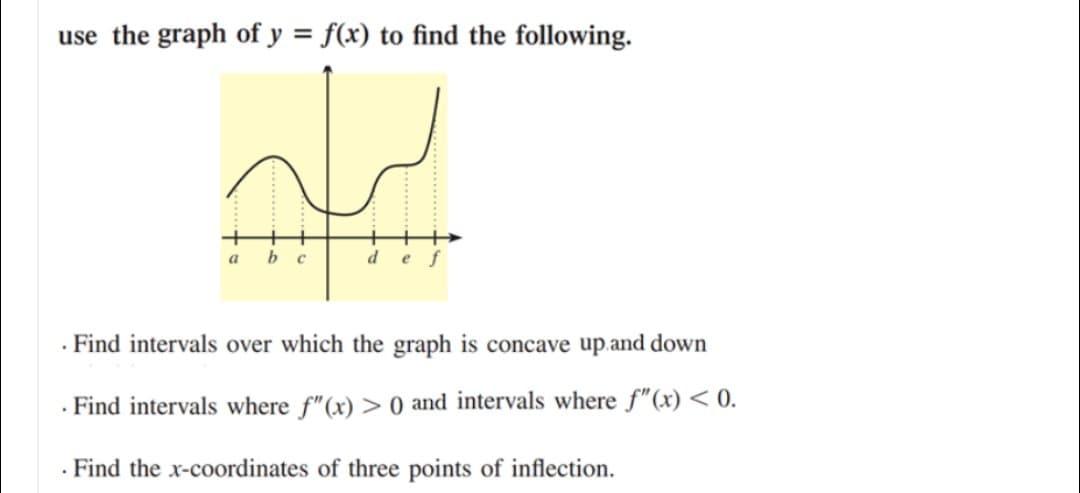



Answered Use The Graph Of Y F X To Find The Bartleby




List The Intervals On Which The Function Is Increasing By Finding Where F Grater Than 0 F X Sin 2x On 0 2pi Study Com



Http Www Berkeleycitycollege Edu Wp Wjeh Files 12 08 Calculus Note App Derivative4 Pdf




Reading The Graph Of A Function Intervals On Which Fx Is Positive Negative Youtube




Finding Decreasing Interval Given The Function Video Khan Academy




Find The Intervals Where F X 0 Or F X 0 As Chegg Com
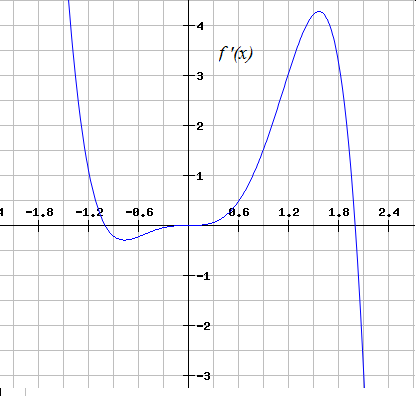



How To Find Increasing Intervals By Graphing Functions Calculus 1
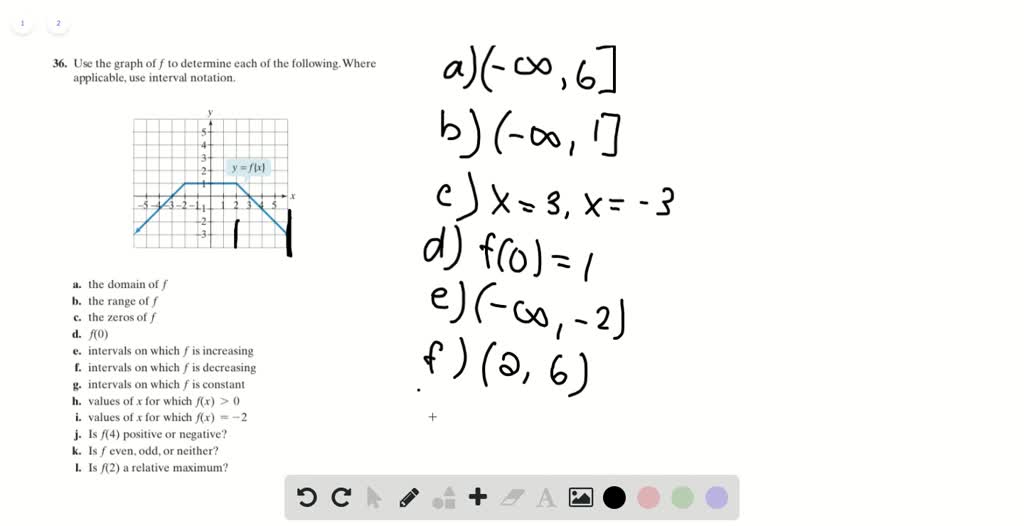



Solved Use The Graph Of F To Determine Each Of The Following Where Applicable Use Interval Notation A The Domain Of



Math 102 Intervals Of Increase And Decrease




4 3 How Derivatives Affect The Shape Of A Graph Facts If F X 0 On An Interval A B Then F X Is Increasing On A B If F X 0 On Ppt Download
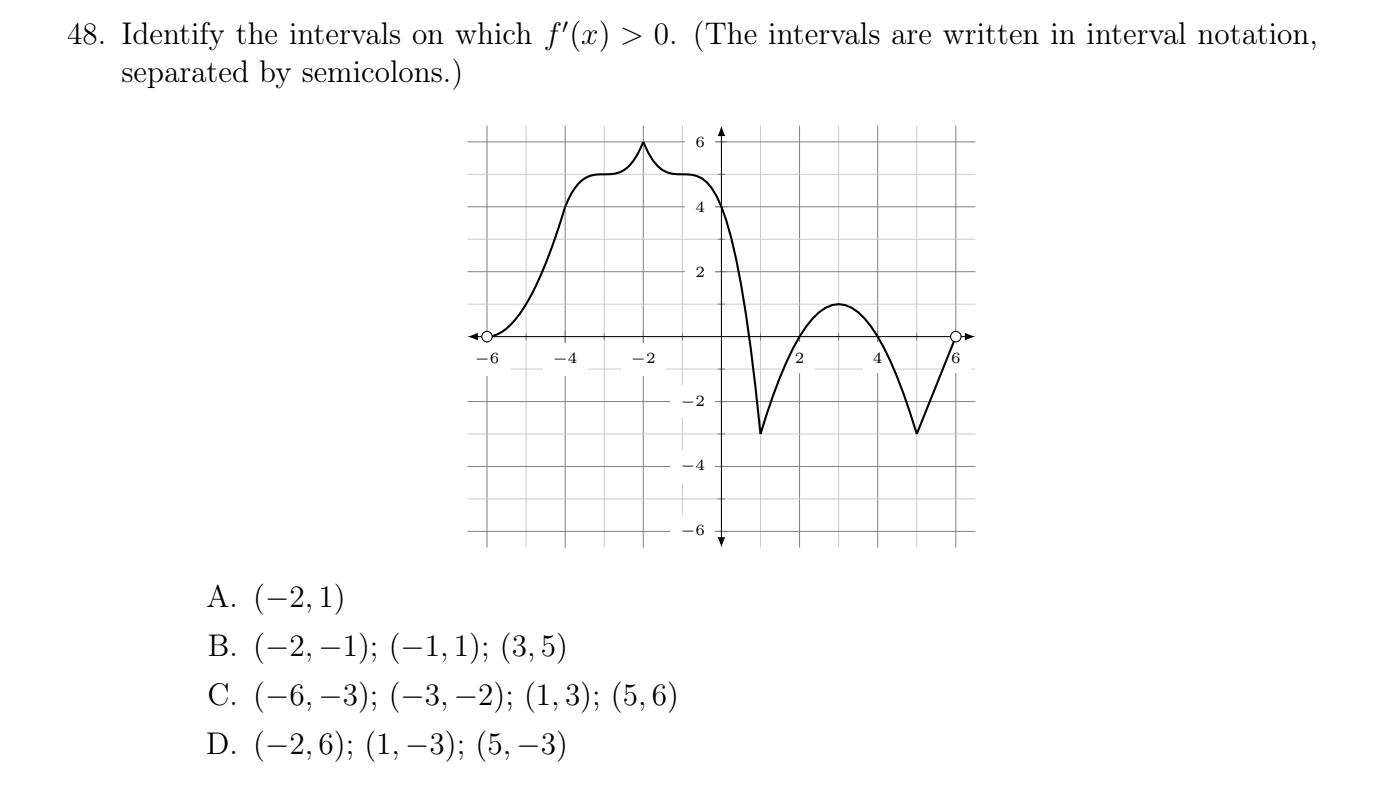



48 Identify The Intervals On Which F X 0 The Chegg Com
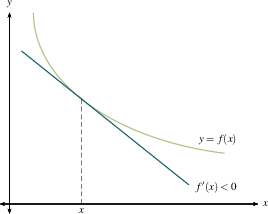



F Vs F




Use The Given Graph Of Y F X To Find The Intervals Chegg Com




If F X 0 On An Interval Then F Is Concave Up On Chegg Com




Question Video Finding The Intervals Of Increasing And Decreasing Of A Rational Function Nagwa




Ex 6 2 4 Find Intervals F X 2x2 3x Is A Increasing




Use The Given Graph Of F X To Find The Intervals On Chegg Com



0 件のコメント:
コメントを投稿